Ermakov convergence criterion

for a series with positive numbers as terms

Let 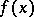be a positive decreasing function for 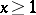. If the inequality

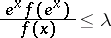holds for these values of with a 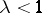, then the series

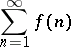converges; if

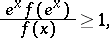then the series diverges. In particular, if the following limit exists and

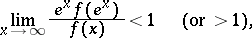then the series converges (diverges). This criterion was established by V.P. Ermakov [1].

References

[1]	V.P. Ermakov, "A new criterion for convergence and divergence of infinite series of constant sign" , Kiev (1872) (In Russian)

References

[a1]	T.J. Bromwich, "An introduction to the theory of infinite series" , Macmillan (1947)