Abel criterion
From Encyclopedia of Mathematics
Abel's criterion for series of numbers. If the series
 |
is convergent and if the numbers 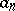 form a monotone bounded sequence, then the series
form a monotone bounded sequence, then the series
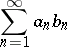 |
is convergent.
Abel's criterion for series of functions. The series
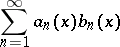 |
converges uniformly on a set 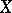 if the series
if the series
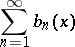 |
converges uniformly on  and if the functions
and if the functions 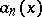 ,
, 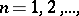 for any
for any 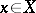 , form a monotone sequence that is uniformly bounded on
, form a monotone sequence that is uniformly bounded on 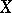 . An Abel criterion for the uniform convergence of integrals
. An Abel criterion for the uniform convergence of integrals
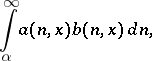 |
which depend on a parameter 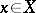 , can be formulated in a similar manner.
, can be formulated in a similar manner.
The Abel criteria can be strengthened (see, for example, Dedekind criterion (convergence of series)). See also Dirichlet criterion (convergence of series); Abel transformation.
References
| [1] | G.M. Fichtenholz, "Differential und Integralrechnung" , 1 , Deutsch. Verlag Wissenschaft. (1964) |
| [2] | L.D. Kudryavtsev, "Mathematical analysis" , 1 , Moscow (1973) (In Russian) |
| [3] | E.T. Whittaker, G.N. Watson, "A course of modern analysis" , 1–2 , Cambridge Univ. Press (1952) |
How to Cite This Entry:
Abel criterion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Abel_criterion&oldid=30926
Abel criterion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Abel_criterion&oldid=30926
This article was adapted from an original article by L.P. Kuptsov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article