Dirichlet criterion (convergence of series)
From Encyclopedia of Mathematics
If a sequence of real numbers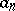 
monotonically tends to zero, and the sequence of partial sums of the series 
is bounded (the terms of this series may also be complex), then the series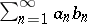 
converges. Established by P.G.L. Dirichlet [1].
References
| [1] | P.G.L. Dirichlet, J. de Math. (2) , 7 (1862) pp. 253–255 |
Comments
How to Cite This Entry:
Dirichlet criterion (convergence of series). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dirichlet_criterion_(convergence_of_series)&oldid=30914
Dirichlet criterion (convergence of series). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dirichlet_criterion_(convergence_of_series)&oldid=30914
This article was adapted from an original article by L.D. Kudryavtsev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article