Dedekind criterion (convergence of series)
From Encyclopedia of Mathematics
The series 
, where 
and 
are complex numbers, converges if the series 
converges absolutely, 
, and if the partial sums of the series 
are bounded.
Comments
The proof is based on the formula of summation by parts: Put 
for 
and 
. Then for 
one has
 |
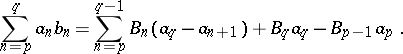A related convergence criterion is the Dirichlet criterion (convergence of series).
References
| [a1] | W. Rudin, "Principles of mathematical analysis" , McGraw-Hill (1953) |
How to Cite This Entry:
Dedekind criterion (convergence of series). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dedekind_criterion_(convergence_of_series)&oldid=30913
Dedekind criterion (convergence of series). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dedekind_criterion_(convergence_of_series)&oldid=30913
This article was adapted from an original article by L.D. Kudryavtsev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article