Complete uniform space
From Encyclopedia of Mathematics
A uniform space in which every Cauchy filter converges. An important example is a complete metric space. A closed subspace of a complete uniform space is complete; a complete subspace of a separable uniform space is closed. The product of complete uniform spaces is complete; conversely, if the product of non-empty uniform spaces is complete, then all the spaces are complete. Any uniform space 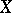 can be uniformly and continuously mapped onto some dense subspace of a complete uniform space
can be uniformly and continuously mapped onto some dense subspace of a complete uniform space  (see Completion of a uniform space).
(see Completion of a uniform space).
References
| [1] | N. Bourbaki, "Elements of mathematics. General topology" , Addison-Wesley (1966) (Translated from French) |
| [2] | J.L. Kelley, "General topology" , Springer (1975) |
Comments
References
| [a1] | J.R. Isbell, "Uniform spaces" , Amer. Math. Soc. (1964) |
How to Cite This Entry:
Complete uniform space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Complete_uniform_space&oldid=30895
Complete uniform space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Complete_uniform_space&oldid=30895
This article was adapted from an original article by M.I. Voitsekhovskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article