Fundamental sequence
From Encyclopedia of Mathematics
Cauchy sequence, of points in a metric space 
A sequence 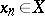 ,
,  such that for any
such that for any  there is a number
there is a number  such that, for all numbers
such that, for all numbers  ,
, 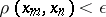 .
.
A generalization of a Cauchy sequence is the concept of a generalized Cauchy sequence (cf. Generalized sequence) in a uniform space. Let  be a uniform space with uniformity
be a uniform space with uniformity  . A generalized sequence
. A generalized sequence  ,
,  , where
, where 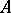 is a directed set, is called a generalized Cauchy sequence if for every element
is a directed set, is called a generalized Cauchy sequence if for every element 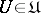 there is an index
there is an index 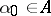 such that for all
such that for all 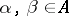 that come after
that come after  in
in 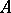 ,
, 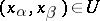 .
.
References
| [1] | P.S. Aleksandrov, "Einführung in die Mengenlehre und die allgemeine Topologie" , Deutsch. Verlag Wissenschaft. (1984) (Translated from Russian) |
| [2] | A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , 1–2 , Graylock (1957–1961) (Translated from Russian) |
| [3] | J.L. Kelley, "General topology" , Springer (1975) |
Comments
Since generalized sequences are also called nets, one also speaks of Cauchy nets in uniform spaces. (Cf. also Net (of sets in a topological space).)
How to Cite This Entry:
Fundamental sequence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fundamental_sequence&oldid=30873
Fundamental sequence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fundamental_sequence&oldid=30873
This article was adapted from an original article by L.D. Kudryavtsev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article