Perimeter
From Encyclopedia of Mathematics
The perimeter of a planar region bounded by a rectifiable curve is the total length of the boundary of this region.
The perimeter of a measurable set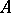 
in an 
-dimensional Euclidean (or Riemannian) space is the lower limit of the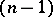 
-dimensional areas of boundaries of polyhedra 
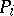(or sets 
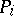with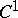 
-smooth boundaries) converging to 
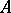in volume, i.e. such that 
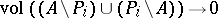as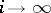 
.
References
| [1a] | R. Caccoppoli, "Misura e integrazione sugli insiemi dimensionalmente orientati I" Rend. Accad. Naz. Lincei Ser. 8 , 12 : 1 (1952) pp. 3–11 |
| [1b] | R. Caccoppoli, "Misura e integrazione sugli insiemi dimensionalmente orientati II" Rend. Accad. Naz. Lincei Ser. 8 , 12 : 2 (1952) pp. 137–146 |
| [2] | E. de Giorgi, "Sulla proprietà isoperimetrica dell'ipersfera, nella classe degli insiemi aventi frontiera orientata di misura finita" Rend. Accad. Naz. Lincei Ser. 1 , 5 : 2 (1958) pp. 33–34 |
Comments
References
| [a1] | E. Giusti, "Minimal surfaces and functions of bounded variation" , Birkhäuser (1984) |
| [a2] | M. Berger, "Geometry" , 1–2 , Springer (1987) (Translated from French) |
| [a3] | Yu.D. Burago, V.A. Zalgaller, "Geometric inequalities" , Springer (1988) (Translated from Russian) |
| [a4] | H. Federer, "Geometric measure theory" , Springer (1969) pp. 60; 62; 71; 108 |
How to Cite This Entry:
Perimeter. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Perimeter&oldid=30848
Perimeter. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Perimeter&oldid=30848
This article was adapted from an original article by V.A. Zalgaller (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article