Peano theorem

One of the existence theorems for solutions of an ordinary differential equation (cf. Differential equation, ordinary), established by G. Peano [1], and consisting in the following. Suppose one is given the differential equation

(*)

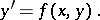If the function 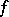is bounded and continuous in a region 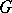, then through each interior point 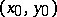of this region there passes at least one integral curve for (*). It may be that more than one integral curve passes through a certain point, e.g. for the equation 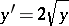there exists an infinite set of integral curves passing through :

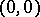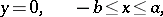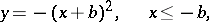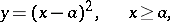where and 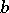are arbitrary constants.

There are generalizations (including multi-dimensional ones) of Peano's theorem (see [2], [3]).

References

[1]	G. Peano, "Démonstration de l'intégrabilité des équations différentielles ordinaires" Math. Ann. , 37 (1890) pp. 182–228
[2]	I.G. Petrovskii, "Ordinary differential equations" , Prentice-Hall (1966) (Translated from Russian)
[3]	P. Hartman, "Ordinary differential equations" , Birkhäuser (1982)