Figure

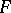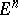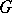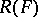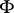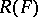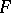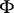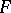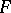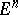A subset of a homogeneous space with fundamental group that can be included in a system of subsets of this space isomorphic to some space of a geometric object (see Geometric objects, theory of). is called the figure space of . The components of are called the coordinates of the associated figure . To each figure in corresponds a class 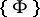of similar geometric objects. The rank, genre, characteristic, and type of a geometric object 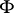in 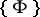are called the rank, genre, characteristic, and type of the figure 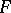(the so-called arithmetic invariants of the figure, cf. [2]). For example, a circle in three-dimensional Euclidean space is a figure of rank 6, genre 1, characteristic 1, and type 1; a point in three-dimensional projective space is a figure of rank 3, genre 0, characteristic 2, and type 1. The completely-integrable system of Pfaffian equations defining the geometric object 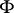is called the stationarity system of equations of .

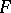Let 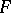and 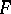be two figures in 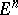. If there is a mapping of 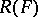onto 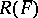under which every geometric object corresponding to 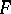is covered by every geometric object corresponding to 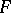, then one says that 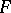covers or induces 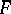( 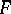is said to be covered or induced by 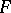). A figure 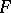of rank 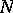is called simple if it does not cover any other figure of lower rank. 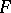is called an inducing figure of index 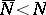if there is a figure of rank 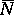that is covered by 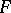, while the rank 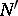of any other figure 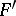covered by 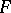does not exceed 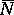. For example, a point, a 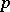-dimensional plane and a hyperquadric in an -dimensional projective space are simple figures, and a hyperquadric in an -dimensional affine space and a 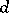-dimensional 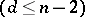quadric in an -dimensional projective space are inducing figures of indices and 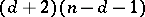, respectively.

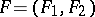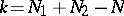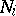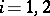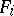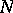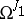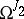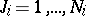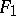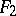An ordered set of two figures, , is called a figure pair. The incidence coefficient of a figure pair is the number , where () is the rank of , and is the rank of the system of forms , , , that are the left-hand sides of the stationarity equations of and . If 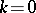, then the pair 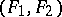is called non-incident.

References

[1]	G.F. Laptev, "Differential geometry of imbedded manifolds. Group-theoretical method of differential-geometric investigation" Trudy Moskov. Mat. Obshch. , 2 (1953) pp. 275–383 (In Russian)
[2]	V.S. Malakhovskii, "Differential geometry of manifolds of figures and of figure pairs" Trudy Geom. Sem. Inst. Nauchn. Inform. Akad. Nauk SSSR , 2 (1969) pp. 179–206 (In Russian)
[3]	V.S. Malakhovskii, "Differential geometry of lines and surfaces" J. Soviet Math. , 2 (1974) pp. 304–330 Itogi Nauk. i Tekhn. Algebra. Topol. Geom. , 10 (1972) pp. 113–158