Serre fibration

A triple 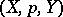, where 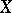and 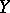are topological spaces and 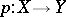is a continuous mapping, with the following property (called the property of the existence of a covering homotopy for polyhedra). For any finite polyhedron 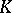and for any mappings

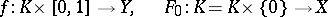with

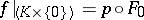there is a mapping

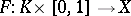such that 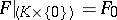, 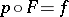. It was introduced by J.-P. Serre in 1951 (see [1]).

References

[1]	J.P. Serre, "Homologie singulière des espaces fibrés. Applications" Ann. of Math. , 54 (1951) pp. 425–505

Comments

A Serre fibration is also called a weak fibration. If the defining homotopy lifting property holds for every space (not just polyhedra), 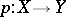is called a fibration or Hurewicz fibre space.

References

[a1]	E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966) pp. Chapt. 2, §2; Chapt. 7, §2