Bilinear mapping
bilinear function
A mapping 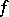 from the product
from the product 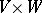 of a left unitary
of a left unitary 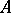 -module
-module 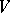 and of right unitary
and of right unitary 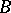 -module
-module 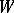 into an
into an 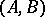 -bimodule
-bimodule 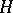 , satisfying the conditions
, satisfying the conditions
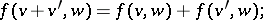 |
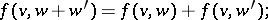 |
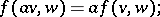 |
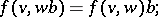 |
where 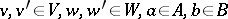 are arbitrarily chosen elements, and
are arbitrarily chosen elements, and 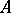 and
and 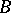 are rings with a unit element. The tensor product
are rings with a unit element. The tensor product 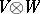 over
over 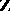 has the natural structure of an
has the natural structure of an 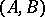 -bimodule. Let
-bimodule. Let 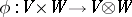 be a canonical mapping; any bilinear mapping
be a canonical mapping; any bilinear mapping 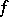 will then induce a homomorphism of
will then induce a homomorphism of 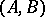 -bimodules
-bimodules 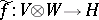 for which
for which 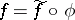 . If
. If 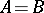 and
and 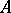 is commutative, then the set
is commutative, then the set 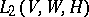 of all bilinear mappings
of all bilinear mappings 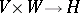 is an
is an 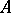 -module with respect to the pointwise defined operations of addition and multiplication with elements in
-module with respect to the pointwise defined operations of addition and multiplication with elements in 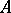 , while the correspondence
, while the correspondence 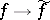 establishes a canonical isomorphism between the
establishes a canonical isomorphism between the 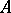 -module
-module 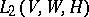 and the
and the 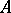 -module
-module 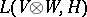 of all linear mappings from
of all linear mappings from 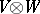 into
into 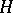 .
.
Let 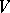 and
and 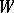 be free modules with bases
be free modules with bases 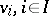 , and
, and 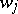 ,
, 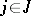 , respectively. A bilinear mapping
, respectively. A bilinear mapping 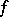 is fully determined by specifying
is fully determined by specifying 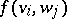 for all
for all 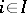 ,
, 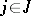 , since for any finite subsets
, since for any finite subsets 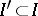 ,
, 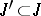 , the following formula is valid:
, the following formula is valid:
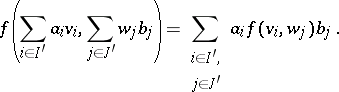 | (*) |
Conversely, after the elements 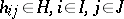 , have been chosen arbitrarily, formula (*), where
, have been chosen arbitrarily, formula (*), where 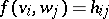 , defines a bilinear mapping from
, defines a bilinear mapping from 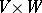 into
into 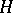 . If
. If 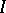 and
and 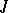 are finite, the matrix
are finite, the matrix 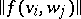 is said to be the matrix of
is said to be the matrix of 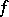 with respect to the given bases.
with respect to the given bases.
Let a bilinear mapping 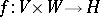 be given. Two elements
be given. Two elements 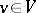 ,
, 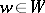 are said to be orthogonal with respect to
are said to be orthogonal with respect to 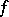 if
if 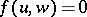 . Two subsets
. Two subsets 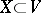 and
and 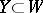 are said to be orthogonal with respect to
are said to be orthogonal with respect to 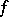 if any
if any 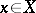 is orthogonal to any
is orthogonal to any 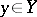 . If
. If 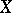 is a submodule in
is a submodule in 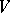 , then
, then
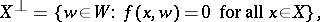 |
which is a submodule of 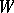 , is called the orthogonal submodule or the orthogonal complement to
, is called the orthogonal submodule or the orthogonal complement to 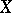 . The orthogonal complement
. The orthogonal complement 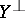 of the submodule
of the submodule 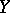 in
in 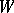 is defined in a similar way. The mapping
is defined in a similar way. The mapping 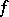 is said to be right-degenerate (left-degenerate) if
is said to be right-degenerate (left-degenerate) if 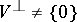 (
(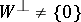 ). The submodules
). The submodules 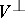 and
and 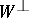 are called, respectively, the left and right kernels of the bilinear mapping
are called, respectively, the left and right kernels of the bilinear mapping 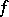 . If
. If 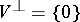 and
and 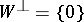 , then
, then 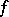 is said to be non-degenerate; otherwise it is said to be degenerate. The mapping
is said to be non-degenerate; otherwise it is said to be degenerate. The mapping 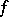 is said to be a zero mapping if
is said to be a zero mapping if 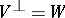 and
and 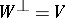 .
.
Let 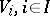 , be a set of left
, be a set of left 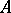 -modules, let
-modules, let 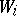 ,
, 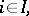 be a set of right
be a set of right 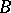 -modules, let
-modules, let 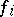 be a bilinear mapping from
be a bilinear mapping from 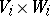 into
into 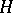 , let
, let 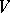 be the direct sum of the
be the direct sum of the 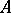 -modules
-modules 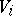 , and let
, and let 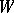 be the direct sum of the
be the direct sum of the 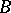 -modules
-modules 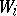 . The mapping
. The mapping 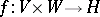 , defined by the rule
, defined by the rule
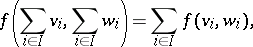 |
is a bilinear mapping and is said to be the direct sum of the mappings 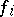 . This is an orthogonal sum, i.e. the submodule
. This is an orthogonal sum, i.e. the submodule 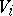 is orthogonal to the submodule
is orthogonal to the submodule 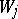 with respect to
with respect to 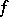 if
if 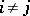 .
.
The bilinear mapping 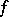 is non-degenerate if and only if
is non-degenerate if and only if 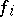 is non-degenerate for all
is non-degenerate for all 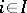 . Moreover, if
. Moreover, if 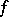 is non-degenerate then one has
is non-degenerate then one has
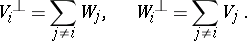 |
If 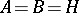 , a bilinear mapping is called a bilinear form.
, a bilinear mapping is called a bilinear form.
References
| [1] | N. Bourbaki, "Elements of mathematics. Algebra: Algebraic structures. Linear algebra" , 1 , Addison-Wesley (1974) pp. Chapt.1;2 (Translated from French) |
| [2] | S. Lang, "Algebra" , Addison-Wesley (1974) |
Bilinear mapping. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bilinear_mapping&oldid=30648