Accumulation point

of a set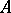

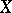A point in a topological space such that in any neighbourhood of there is a point of 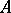distinct from . A set can have many accumulation points; on the other hand, it can have none. For example, any real number is an accumulation point of the set of all rational numbers in the ordinary topology. In a discrete space, no set has an accumulation point. The set of all accumulation points of a set 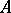in a space 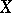is called the derived set (of 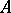). In a 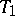-space, every neighbourhood of an accumulation point of a set contains infinitely many points of the set.

The concept just defined should be distinguished from the concepts of a proximate point and a complete accumulation point. In particular, any point of a set is a proximate point of the set, while it need not be an accumulation point (a counterexample: any point in a discrete space).