Lambert summation method
From Encyclopedia of Mathematics
A method for summing series of numbers. The series
 |
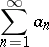is summable by Lambert's method to the number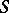 
if
 |
where
 |
and if the series on the right-hand side converges. The method was proposed by J.H. Lambert [1]. The summability of a series by the Cesàro summation method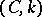 
for some 
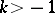(cf. Cesàro summation methods) to the sum 
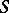implies its summability by the Lambert method to the same sum, and if the series is summable by the Lambert method to the sum 
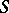, then it is also summable by the Abel summation method to the same sum. Lambert's summation method is regular (see Regular summation methods).
References
| [1] | J.H. Lambert, "Anlage zur Architektonik" , 2 , Riga (1771) |
| [2] | G.H. Hardy, "Divergent series" , Clarendon Press (1949) |
How to Cite This Entry:
Lambert summation method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lambert_summation_method&oldid=30239
Lambert summation method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lambert_summation_method&oldid=30239
This article was adapted from an original article by I.I. Volkov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article