Improper integral

An integral of an unbounded function or of a function over an unbounded set. Suppose that 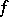is a function defined on a finite or infinite half-interval 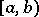, , 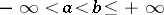and that 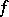, for every 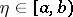, is Riemann- (or Lebesgue-) integrable on 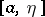. Then the limit

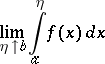(1)

(when 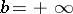, the condition 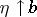is understood as 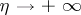) is called the improper integral

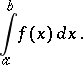If the limit (1) exists and is finite, then one says that the improper integral converges and if not, that it diverges. For example, the improper integral

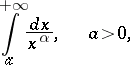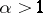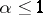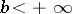converges for and diverges . If , then

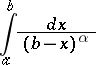converges for 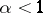and diverges for .

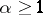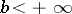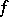If and is Riemann- (or Lebesgue-) integrable on 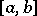, then the improper integral (1) is the same as the definite integral.

Similarly, under the corresponding assumptions one defines the improper integral over , ,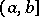

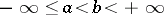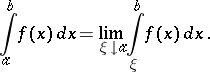(2)

If 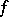is Riemann- (or Lebesgue-) integrable over every interval 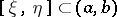, if 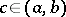and if the improper integrals

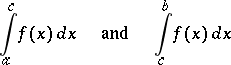both converge, then the improper integral

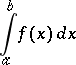is defined as their sum,

and does not depend on the choice of .

If on 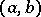there are finitely many points 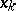(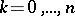), , 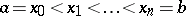such that 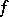is Riemann- (or Lebesgue-) integrable on every interval 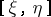that does not contain any point 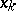and if for every 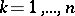the improper integral

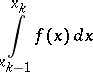converges, then

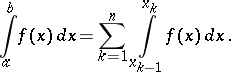This definition does not depend on the position of the points .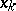

The general properties of integrals carry over to improper integrals: linearity, additivity with respect to the intervals over which the integration proceeds, the rule for integrating inequalities, the mean-value theorems, integration by parts, change of variable, and the Newton–Leibniz formula. For example, if 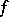coincides almost-everywhere on 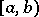with the derivative of a function 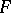that is absolutely continuous on every 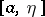, , 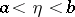then

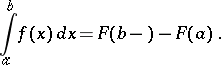To decide about the convergence of the indefinite integral of functions of constant sign one uses the comparison test. E.g., for an indefinite integral of the form (1), when

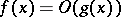as 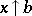, , 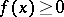, , 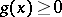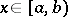then the convergence of the improper integral

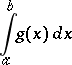implies that of

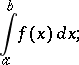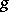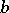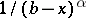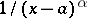in this case is called a comparison function. As a comparison function for integrals (1) in the case of a finite integration limit one often uses ; for integrals of the form (2) in the case of a finite integration limit — the function ; and when there are one or two infinite integration limits — the function 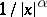. For example, when for a non-negative function 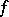defined for 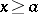the limit

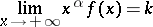exists, the comparison test implies that for 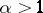and 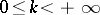the improper integral

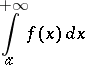of the form (1) converges while for 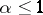and 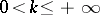it diverges.

A necessary and sufficient condition for the convergence of an improper integral is given by Cauchy's criterion. I.e., an improper integral of the form (1) converges if and only if for every 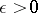there is an 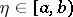such that for all ,

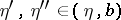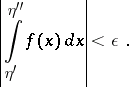An improper integral

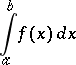is said to be absolutely convergent if the improper integral

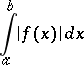converges. If an improper integral converges absolutely, then it converges and coincides with the Lebesgue integral. There exist improper integrals that converge, but not absolutely. For example, for a finite interval:

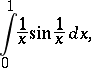and for an infinite interval:

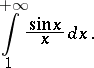There are several tests to establish the convergence of an improper integral. E.g., if 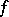and 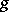are defined for 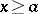, if 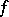has on 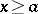a bounded primitive, and if 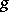is a monotone function tending to zero as 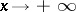, then the improper integral

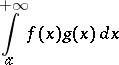converges. Another test: If the improper integral

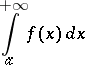converges and if 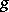is monotone and bounded for 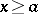, then the improper integral

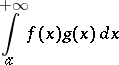converges.

The convergence of an improper integral can be expressed in terms of the convergence of series. For example, for an improper integral (1) to converge it is necessary and sufficient that for any sequence 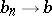, , 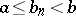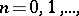the series

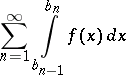converges, and if it converges, then the sum of the series is the same as the value of the improper integral (1).

The concept of an improper integral has been generalized to functions of several variables. Suppose that 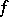is defined on an open (bounded or unbounded) set 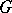of the -dimensional Euclidean space 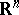and is Riemann-integrable over any Jordan-measurable set 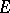, 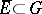. Then 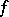is said to be integrable in the improper sense over 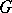if for any sequence of Jordan-measurable sets 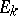such that 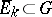, , 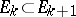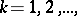and 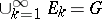, the limit

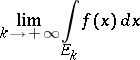exists and is independent of the choice of the sequence 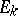. This limit, if it exists and is finite, is called the improper integral

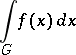and, as in the one-dimensional case, one says that this integral converges. It converges if and only if the integral

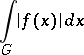is finite. In this case the improper integral

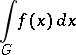is the same as the Lebesgue integral. This is connected with the fact that, for 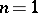and the definition of an improper integral given above, the limit transition is over a very special class of Jordan-measurable sets, namely intervals. The 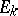were taken as arbitrary Jordan-measurable sets. However, for 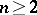the assertion remains valid when the are taken to be any Jordan-measurable domains. Thus, in this case the concept of an improper integral does not lead to anything new as compared with the Lebesgue integral.

For improper integrals of functions of several variables a comparison test holds, similar to the one-dimensional case. The integrals

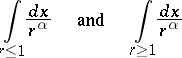are taken as comparison integrals, where

The former converges for 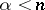and diverges for 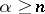, the latter converges for 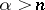and diverges for .

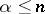Integrals in the sense of the principal value belong to the improper integrals. Suppose that a function 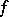is defined on an open set 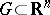except possibly at a point 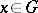and suppose that, for any 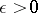, 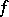is (Riemann- or Lebesgue-) integrable over 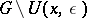, where 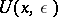is the -neighbourhood of . If the limit

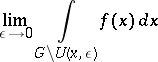exists, then it is called the integral in the sense of the principal value (or principal-value integral) of 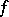, and is denoted by

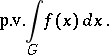If

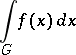exists as an improper integral, then it also exists in the sense of the principal value. The converse is not true, in general. For example, the improper integral

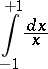diverges, whereas

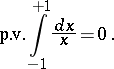Similarly one defines integrals in the sense of the principal value at the point at infinity.

References

[1]	V.A. Il'in, E.G. Poznyak, "Fundamentals of mathematical analysis" , 2 , MIR (1982) (Translated from Russian)
[2]	L.D. Kudryavtsev, "A course in mathematical analysis" , 2 , Moscow (1988) (In Russian)
[3]	S.M. Nikol'skii, "A course of mathematical analysis" , 2 , MIR (1977) (Translated from Russian)

Comments

Instead of "principal value (integral)" one often says Cauchy principal value (integral). It is also denoted by .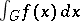

For the method of residues, cf. Complex integration, method of.

A proof of the fact (mentioned above) that a multi-dimensional improper integral of a function 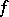over a region 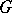exists if and only if exists, can be found in, e.g., [a5].

An example of a function integrable in the improper sense is the functi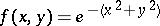on on .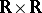

References

[a1]	G.E. Shilov, "Mathematical analysis" , 1–2 , M.I.T. (1974) (Translated from Russian)
[a2]	G.H. Hardy, "A course of pure mathematics" , Cambridge Univ. Press (1975)
[a3]	L. Schwartz, "Méthodes mathématiques pour les sciences physiques" , Hermann (1965)
[a4]	R.C. Buck, "Advanced calculus" , McGraw-Hill (1965)
[a5]	G. Valiron, "Théorie des fonctions" , Masson (1948) pp. 287ff
[a6]	T.M. Apostol, "Calculus" , 1–2 , Blaisdell (1969)
[a7]	T.M. Apostol, "Mathematical analysis" , Addison-Wesley (1963)
[a8]	W. Rudin, "Real and complex analysis" , McGraw-Hill (1974) pp. 24
[a9]	A.C. Zaanen, "Integration" , North-Holland (1967)