Summable function
From Encyclopedia of Mathematics
A function 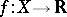 , where
, where 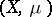 is a space with a non-negative measure, for which the Lebesgue integral
is a space with a non-negative measure, for which the Lebesgue integral 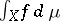 is defined and finite. The set of summable functions
is defined and finite. The set of summable functions 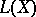 forms a linear subspace of the space of measurable functions. Taking the absolute value of a function and the maximum and minimum of a finite system of functions does not lead outside
forms a linear subspace of the space of measurable functions. Taking the absolute value of a function and the maximum and minimum of a finite system of functions does not lead outside 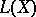 . If
. If 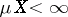 , then
, then 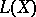 is closed in the sense of uniform convergence.
is closed in the sense of uniform convergence.
Comments
A standard notation for the space of summable or Lebesgue integrable functions on 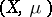 is
is 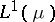 or
or 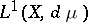 (or
(or 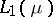 ,
, 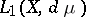 ).
).
References
| [a1] | W. Rudin, "Real and complex analysis" , McGraw-Hill (1966) pp. 24 |
| [a2] | G.E. Shilov, B.L. Gurevich, "Integral, measure, and derivative: a unified approach" , Dover, reprint (1977) pp. 29ff (Translated from Russian) |
How to Cite This Entry:
Summable function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Summable_function&oldid=29893
Summable function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Summable_function&oldid=29893
This article was adapted from an original article by I.A. Vinogradova (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article