Mechanical quadrature, method of

method of mechanical cubature

A method for solving integral equations, based on replacing an integral by a sum using quadrature (cubature) formulas. Consider the equation

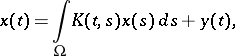(1)

where 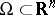is a bounded open domain. Using a quadrature (cubature) process

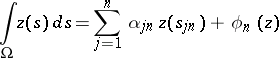one forms the system of linear equations

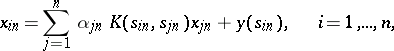(2)

where , .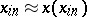

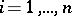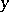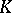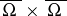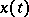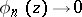Let the absolute term and the kernel be continuous on and , respectively ( is the closure of ), and let (1) have a unique solution . Let as 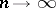for any continuous functi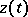on on . Then for sufficiently large the system (2) is uniquely solvable and

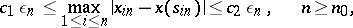where 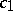and 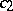are positive constants and

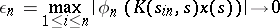as .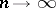

A mechanical quadrature method can be applied for the solution of non-linear integral equations [3] and eigen value problems for linear operators. The method converges even for a certain class of equations with discontinuous kernels [4].

References

[1]	V.I. Krylov, V.V. Bobkov, P.I. Monastyrnyi, "Numerical methods" , 2 , Moscow (1977) (In Russian)
[2]	I.S. Berezin, N.P. Zhidkov, "Computing methods" , Pergamon (1973) (Translated from Russian)
[3]	M.A. Krasnosel'skii, G.M. Vainikko, P.P. Zabreiko, et al., "Approximate solution of operator equations" , Wolters-Noordhoff (1972) (Translated from Russian)
[4]	G.M. Vainikko, "On the convergence of the method of mechanical quadratures for integral equations with discontinuous kernels" Sib. Math. J. , 12 : 1 (1971) pp. 29–38 Sibirsk. Mat. Zh. , 12 : 1 (1971) pp. 40–53
[5]	S.G. [S.G. Mikhlin] Michlin, S. Prössdorf, "Singular integral operators" , Springer (1986) (Translated from German)

References

[a1]	H. Brunner, P.J. van der Houwen, "The numerical solution of Volterra equations" , North-Holland (1986)
[a2]	C.T.H. Baker, "The numerical treatment of integral equations" , Clarendon Press (1977) pp. Chapt. 4
[a3]	H. Engels, "Numerical quadrature and cubature" , Acad. Press (1980)
[a4]	K.E. Atkinson, "A survey of numerical methods for the solution of Fredholm integral equations of the second kind" , SIAM (1976)