Taylor polynomial
of degree  , for a function
, for a function 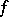 that is
that is  times differentiable at
times differentiable at 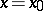
The polynomial
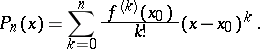 |
The values of the Taylor polynomial and of its derivatives up to order  inclusive at the point
inclusive at the point 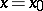 coincide with the values of the function and of its corresponding derivatives at the same point:
coincide with the values of the function and of its corresponding derivatives at the same point:
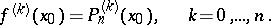 |
The Taylor polynomial is the best polynomial approximation of the function 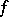 as
as 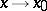 , in the sense that
, in the sense that
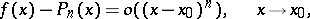 | (*) |
and if some polynomial 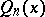 of degree not exceeding
of degree not exceeding  has the property that
has the property that
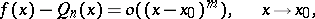 |
where 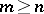 , then it coincides with the Taylor polynomial
, then it coincides with the Taylor polynomial 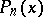 . In other words, the polynomial having the property (*) is unique.
. In other words, the polynomial having the property (*) is unique.
If at least one of the derivatives 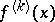 ,
, 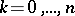 , is not equal to 0 at the point
, is not equal to 0 at the point 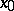 , then the Taylor polynomial is the principal part of the Taylor formula.
, then the Taylor polynomial is the principal part of the Taylor formula.
Comments
For references see Taylor formula.
Taylor polynomial. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Taylor_polynomial&oldid=29524