Lobachevskii criterion (for convergence)
From Encyclopedia of Mathematics
A series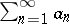 
with positive terms 
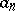tending monotonically to zero converges or diverges according as the series
 |
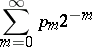converges or diverges, where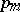 
is the largest of the indices of the terms 
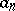that satisfy the inequality 
, 
.
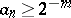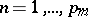It was proposed by N.I. Lobachevskii in 1834–1836.
How to Cite This Entry:
Lobachevskii criterion (for convergence). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lobachevskii_criterion_(for_convergence)&oldid=29181
Lobachevskii criterion (for convergence). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lobachevskii_criterion_(for_convergence)&oldid=29181
This article was adapted from an original article by V.I. Bityutskov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article