Leibniz criterion
From Encyclopedia of Mathematics
for convergence of an alternating series
If the terms of an alternating series
 |
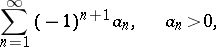decrease monotonically (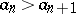
, 
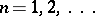) and tend to zero (
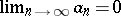), then the series converges; moreover, a remainder of the series,
 |
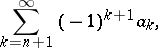has the sign of its first term and is less than it in absolute value. The criterion was established by G. Leibniz in 1682.
Comments
References
| [a1] | K. Knopp, "Theorie und Anwendung der unendlichen Reihen" , Springer (1964) (English translation: Blackie, 1951 & Dover, reprint, 1990) |
How to Cite This Entry:
Leibniz criterion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Leibniz_criterion&oldid=29175
Leibniz criterion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Leibniz_criterion&oldid=29175
This article was adapted from an original article by V.I. Bityutskov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article