Quadratic equation

An algebraic equation of the second degree. The general form of a quadratic equation is

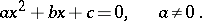In the field of complex numbers a quadratic equation has two solutions, expressed by radicals in the coefficients of the equation:

(*)

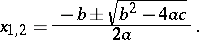When both solutions are real and distinct, when , they are complex (complex-conjugate) numbers, when 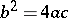the equation has the double root .

For the reduced quadratic equation

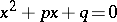formula (*) has the form

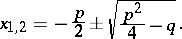The roots and coefficients of a quadratic equation are related by (cf. Viète theorem):

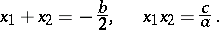Comments

The expression is called the discriminant of the equation. It is easily proved that , in accordance with the fact mentioned above that the equation has a double root if and only if . See also Discriminant. Formula (*) holds also if the coefficients belong to a field with characteristic different from 2.

Formula (*) follows from writing the left-hand side of the equation as 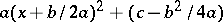(splitting of the square).

References

[a1]	K. Rektorys (ed.) , Applicable mathematics , Iliffe (1969) pp. Sect. 1.20