Riemann hypotheses
From Encyclopedia of Mathematics
in analytic number theory
Five conjectures, formulated by B. Riemann (1876), concerning the distribution of the non-trivial zeros of the zeta-function 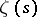 , and the expression via these zeros of the number of prime numbers not exceeding a real number
, and the expression via these zeros of the number of prime numbers not exceeding a real number  . One of the Riemann hypotheses has neither been proved nor disproved: All non-trivial zeros of the zeta-function
. One of the Riemann hypotheses has neither been proved nor disproved: All non-trivial zeros of the zeta-function 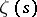 lie on the straight line
lie on the straight line 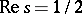 .
.
Comments
For the list of all 5 conjectures see Zeta-function.
References
| [a1] | A. Ivic, "The Riemann zeta-function" , Wiley (1985) |
| [a2] | E.C. Titchmarsh, "The theory of the Riemann zeta-function" , Clarendon Press (1951) |
| [a3] | H.M. Edwards, "Riemann's zeta function" , Acad. Press (1974) pp. Chapt. 3 |
How to Cite This Entry:
Riemann hypotheses. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Riemann_hypotheses&oldid=29141
Riemann hypotheses. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Riemann_hypotheses&oldid=29141
This article was adapted from an original article by A.F. Lavrik (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article