Parabolic spiral

A transcendental plane curve whose equation in polar coordinates has the form

To each value of 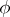correspond two values of 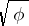, one positive and one negative.

Figure: p071250a

The curve has infinitely many double points and one point of inflection (see Fig.). If 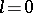, then the curve is called the Fermat spiral. The parabolic spiral is related to the so-called algebraic spirals (see Spirals).

References

[1]	A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian)

References

[a1]	F. Gomez Teixeira, "Traité des courbes" , 1–3 , Chelsea, reprint (1971)
[a2]	J.D. Lawrence, "A catalog of special plane curves" , Dover, reprint (1972)