Tight measure
From Encyclopedia of Mathematics
Let 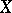 be a topological space,
be a topological space,  the Borel
the Borel 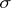 -field generated by the open sets and
-field generated by the open sets and 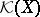 the paving (i.e. family of subsets) of all compact sets. A measure
the paving (i.e. family of subsets) of all compact sets. A measure 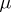 on
on 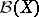 is tight if
is tight if
 |
A finite tight measure on 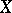 is a Radon measure. If
is a Radon measure. If 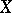 is a separable complete metric space, every probability measure on
is a separable complete metric space, every probability measure on 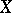 is tight (Ulam's tightness theorem), [a2]. The terminology "tight" was introduced by L. LeCam, [a5].
is tight (Ulam's tightness theorem), [a2]. The terminology "tight" was introduced by L. LeCam, [a5].
More generally, let 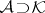 be two pavings on a set
be two pavings on a set 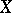 , and
, and 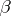 a set function defined on
a set function defined on  . Then
. Then 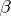 is tight with respect to
is tight with respect to 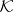 if
if
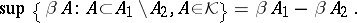 |
References
| [a1] | P. Billingsley, "Convergence of probability measures" , Wiley (1968) pp. 9ff |
| [a2] | F. Topsøe, "Topology and measure" , Springer (1970) pp. xii |
| [a3] | K. Bichteler, "Integration theory (with special attention to vector measures)" , Lect. notes in math. , 315 , Springer (1973) pp. §24 |
| [a4] | J.C. Oxtoby, S. Ulam, "On the existence of a measure invariant under a transformation" Ann. of Math. , 40 (1939) pp. 560–566 |
| [a5] | L. LeCam, "Convergence in distribution of probability processes" Univ. of Calif. Publ. Stat. , 2 : 11 (1957) pp. 207–236 |
How to Cite This Entry:
Tight measure. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Tight_measure&oldid=28960
Tight measure. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Tight_measure&oldid=28960