Support of a function
From Encyclopedia of Mathematics
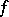defined on a topological space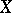 
The smallest closed set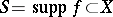 
such that the values of the numerical function 
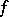are zero everywhere on the complement 
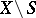. In other words, 
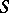is the closure of the set of all points 
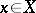for which 
.
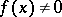Comments
A function is said to be of compact support if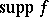 
is compact. The functions of compact support with values in 
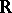, or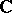 
(or other rings or fields), form a vector space.
References
| [a1] | W. Rudin, "Real and complex analysis" , McGraw-Hill (1966) pp. 38 |
How to Cite This Entry:
Support of a function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Support_of_a_function&oldid=28948
Support of a function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Support_of_a_function&oldid=28948
This article was adapted from an original article by E.D. Solomentsev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article