Field of sets
From Encyclopedia of Mathematics
A collection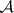 
of subsets of a set 
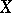satisfying:
i)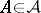 
implies 
;
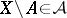ii)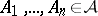 
implies 
, 
.
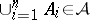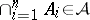A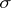 
-field of sets is a field of sets satisfying in addition
a)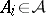 
, 
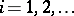, implies 
, 
.
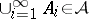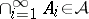A 
-field is also sometimes called a Borel field of sets.
Sometimes, an algebra (respectively, a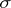 
-algebra) of sets is taken to mean a field (respectively, a 
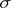-field) of sets.
References
| [a1] | M. Loeve, "Probability theory" , v. Nostrand (1963) pp. 59 (Edition: Third) |
| [a2] | H. Bauer, "Probability theory and elements of measure theory" , Holt, Rinehart&Winston (1972) pp. 7 |
How to Cite This Entry:
Field of sets. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Field_of_sets&oldid=28889
Field of sets. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Field_of_sets&oldid=28889
This article was adapted from an original article by M. Hazewinkel (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article