Measurable set

A subset of a measurable space 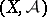belonging to 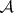, where 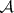is a ring or 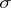-ring of subsets of 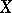. The concept arose and was developed in the process of the solution and generalization of the measurement of areas (lengths, volumes) of various sets; that is, the problem of the extension of area (length, volume) as an additive function of polygons (segments, polyhedra) to a wider system of sets. A measurable set was defined to be a set in the system to which the extension can be realized; this extension is said to be the measure. Thus were defined the Jordan measure, the Borel measure and the Lebesgue measure, with sets measurable according to Jordan, Borel and Lebesgue, respectively. The solution of the problem of extending any fixed measure in 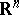led to the Radon measure (Lebesgue–Stieltjes measure) and sets measurable with respect to the Radon (Lebesgue–Stieltjes) measure. The measurable sets connected with a measure defined on an abstract set are the sets on which the measure under discussion is defined.

References

[1]	A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , 1–2 , Graylock (1957–1961) (Translated from Russian)
[2]	P.R. Halmos, "Measure theory" , v. Nostrand (1950)

References

[a1]	E. Hewitt, K.R. Stromberg, "Real and abstract analysis" , Springer (1965)