Lebesgue theorem

Lebesgue's theorem in dimension theory: For any 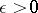the -dimensional cube has a finite closed -covering of multiplicity 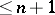, and at the same there is an 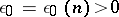such that any finite closed 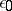-covering of the -dimensional cube has multiplicity 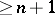(cf. also Covering (of a set)). This assertion led later to a definition of a fundamental dimension invariant, the Lebesgue dimension 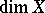of a normal topological space .

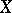Comments

This theorem is also called the Lebesgue covering theorem or "PflastersatzPflastersatz" (see Dimension). In the language of dimension theory it says that 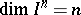for every .

References

[a1]	R. Engelking, "Dimension theory" , North-Holland & PWN (1978) pp. 19; 50
[a2]	W. Hurevicz, G. Wallman, "Dimension theory" , Princeton Univ. Press (1948) ((Appendix by L.S. Pontryagin and L.G. Shnirel'man in Russian edition.))
[a3]	C. Kuratowski, "Introduction to set theory and topology" , Pergamon (1972) (Translated from Polish)

Lebesgue's theorem on the passage to the limit under the integral sign: Suppose that on a measurable set 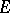there is specified a sequence of measurable functions 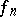that converges almost-everywhere (or in measure) on 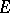to a function 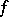. If there is a summable functi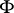on on 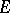such that for all and ,

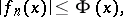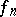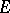then and are summable on and

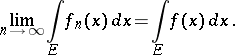This was first proved by H. Lebesgue [1]. The important special case when 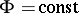and has finite measure is also called the Lebesgue theorem; he obtained it earlier [2].

A theorem first proved by B. Levi [3] is sometimes called the Lebesgue theorem: Suppose that on a measurable set 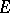there is specified a non-decreasing sequence of measurable non-negative functions 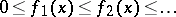(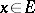) and that

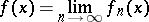almost-everywhere; then

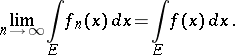References

[1]	H. Lebesgue, "Sur les intégrales singuliéres" Ann. Fac. Sci. Univ. Toulouse Sci. Math. Sci. Phys. , 1 (1909) pp. 25–117
[2]	H. Lebesgue, "Intégrale, longueur, aire" , Univ. Paris (1902) (Thesis)
[3]	B. Levi, "Sopra l'integrazione delle serie" Rend. Ist. Lombardo sue Lett. (2) , 39 (1906) pp. 775–780
[4]	S. Saks, "Theory of the integral" , Hafner (1952) (Translated from French)
[5]	I.P. Natanson, "Theory of functions of a real variable" , 1–2 , F. Ungar (1955–1961) (Translated from Russian)

T.P. Lukashenko

Comments

This Lebesgue theorem is also called the dominated convergence theorem, while Levi's theorem is also known as the monotone convergence theorem.

References

[a1]	N. Dunford, J.T. Schwartz, "Linear operators" , 1–3 , Interscience (1958–1971)
[a2]	P.R. Halmos, "Measure theory" , v. Nostrand (1950)
[a3]	E. Hewitt, K.R. Stromberg, "Real and abstract analysis" , Springer (1965)