Fatou theorem (on Lebesgue integrals)

A theorem on passing to the limit under a Lebesgue integral: If a sequence of measurable (real-valued) non-negative functions converges almost-everywhere on a set to a function , then

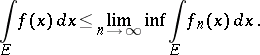It was first proved by P. Fatou [1]. In the statement of it is often replaced by .

References

[1]	P. Fatou, "Séries trigonométriques et séries de Taylor" Acta Math. , 30 (1906) pp. 335–400
[2]	S. Saks, "Theory of the integral" , Hafner (1952) (Translated from French)
[3]	I.P. Natanson, "Theorie der Funktionen einer reellen Veränderlichen" , H. Deutsch , Frankfurt a.M. (1961) (Translated from Russian)

Comments

This result is usually called Fatou's lemma. It holds in a more general form: If is a measure space, is -measurable for and for 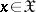, then

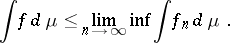It is not necessary that the sequence converges.

References

[a1]	E. Hewitt, K.R. Stromberg, "Real and abstract analysis" , Springer (1965)
[a2]	P.R. Halmos, "Measure theory" , v. Nostrand (1950)