Energy integral
A quantity representing the sum of the kinetic and the potential energy of a mechanical system at a certain moment in time.
Suppose, for example, that in a bounded domain 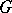 with piecewise-smooth boundary
with piecewise-smooth boundary 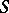 for a hyperbolic partial differential equation
for a hyperbolic partial differential equation
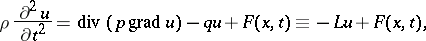 | (1) |
where
 |
one poses the mixed problem
 | (2) |
 | (3) |
 |
A classical solution of (2)–(3) is a function  of class
of class 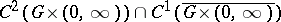 satisfying (1) in the cylinder
satisfying (1) in the cylinder 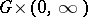 , the initial conditions (2) on the lower base, and the boundary condition (3) on the lateral surface of the cylinder.
, the initial conditions (2) on the lower base, and the boundary condition (3) on the lateral surface of the cylinder.
Then the relation
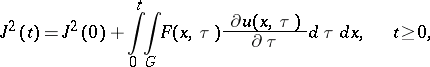 | (4) |
holds, where
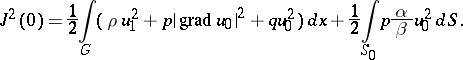 |
The energy integral is defined as the quantity
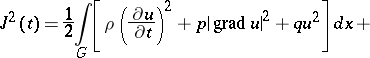 |
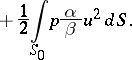 |
For  equality (4) takes the form
equality (4) takes the form
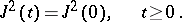 |
The physical meaning of the energy integral consists in the fact that the total energy of an oscillating system in the absence of external perturbations does not change in time (the law of conservation of energy).
References
| [1] | V.S. Vladimirov, "Equations of mathematical physics" , MIR (1984) (Translated from Russian) |
Comments
References
| [a1] | O.A. Ladyzhenskaya, N.N. Ural'tseva, "Equations aux dérivées partielles de type elliptique" , Dunod (1969) (Translated from Russian) |
| [a2] | O.A. Ladyzhenskaya, V.A. Solonnikov, N.N. Ural'tseva, "Linear and quasi-linear equations of parabolic type" , Amer. Math. Soc. (1968) (Translated from Russian) |
| [a3] | L. Bers, F. John, M. Schechter, "Partial differential equations" , Interscience (1966) |
| [a4] | F. John, "Partial differential equations" , Springer (1978) |
| [a5] | P.R. Garabedian, "Partial differential equations" , Wiley (1967) |
Energy integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Energy_integral&oldid=28187