Convex functional

A functional, defined on a convex subset of a linear vector space, the supergraph of which is a convex set. A functional 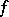which does not assume the value 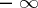on a convex set 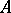is convex on 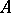if and only if the inequality

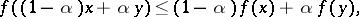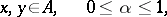is satisfied. If the inequality sign is reversed, the functional 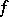is called concave. Operations which convert a convex functional into a convex functional include addition 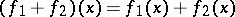, multiplication by a positive number, taking the upper bound

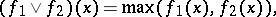and the infimal convolution

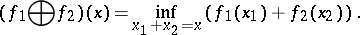A convex functional bounded from above in a neighbourhood of some point is continuous at that point. If a convex functional is finite at some point , it has a (finite or infinite) derivative in any direction at that point. Closed convex functionals (i.e. functionals with convex and closed supergraphs) in locally convex linear topological spaces may be described in a dual way: Such a functional is the least upper bound of the affine functions which it dominates. This duality makes it possible to relate to each convex functional a dual object, the conjugate functional

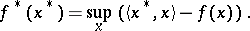Properties of convex functionals, operations on such functionals, and the relationship between a convex functional and its conjugate, are studied in convex analysis.

References

[1]	Z.W. Birnbaum, W. Orlicz, "Ueber die Verallgemeinerung des Begriffes der zueinander konjugierter Potenzen" Studia Math. , 3 (1931) pp. 1–67
[2]	G.H. Hardy, J.E. Littlewood, G. Pólya, "Inequalities" , Cambridge Univ. Press (1934)
[3]	M.A. Krasnosel'skii, Ya.B. Rutitskii, "Convex functions and Orlicz spaces" , Noordhoff (1961) (Translated from Russian)
[4]	W. Fenchel, "On conjugate convex functions" Canad. J. Math. , 1 (1949) pp. 73–77
[5]	R.T. Rockafellar, "Convex analysis" , Princeton Univ. Press (1970)