Ring of sets
From Encyclopedia of Mathematics
A collection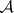 
of subsets of a set 
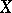satisfying:
i)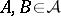 
implies 
;
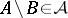ii)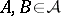 
implies 
.
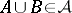It follows that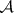 
is also closed under finite intersections, since 
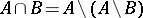. If 
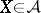, the ring of sets is an algebra of sets.
A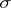 
-ring of sets is a ring of sets satisfying additionally
a)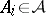 
, 
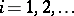, implies 
.
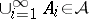A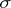 
-ring is closed under countable intersections. If 
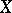is a member of a 
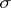-ring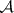 
of subsets of 
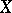, then 
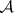is a 
-algebra (cf. Additive class of sets; Algebra of sets).
References
| [a1] | H.R. Pitt, "Integration, measure and probability" , Oliver&Boyd (1963) pp. 2–3 |
How to Cite This Entry:
Ring of sets. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ring_of_sets&oldid=28038
Ring of sets. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ring_of_sets&oldid=28038
This article was adapted from an original article by M. Hazewinkel (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article