Pierpont variation

One of the numerical characteristics of a function of several variables which can be considered as a multi-dimensional analogue of the variation of a function of one variable. Let a function , be given on an -dimensional parallelopipedon

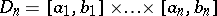and let , , be a subdivision of the segment into , equal segments by points

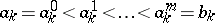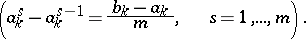These subdivisions generate a subdivision

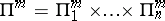of the parallelopipedon 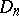into 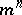parallelopipeda 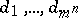with edges parallel to the coordinate axes.

Let

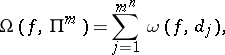where 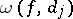is the oscillation of the functi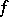on on 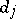(cf. Oscillation of a function). Then

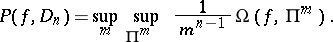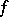If , then the function is said to be of bounded (finite) Pierpont variation on , and the class of all such functions is denoted by . This definition was suggested by J. Pierpont [1]. The class 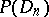contains as a subset the class of all functions of bounded Arzelà variation on .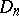

References

[1]	J. Pierpont, "Lectures on the theory of functions of real variables" , 1 , Dover, reprint (1959)
[2]	H. Hahn, "Reellen Funktionen" , 1 , Chelsea, reprint (1948)