One of the numerical characteristics of a function of several variables. It may be considered as a multi-dimensional analogue of the variation of a function of one variable. Let the function 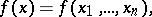
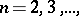 be defined on an
be defined on an  -dimensional parallelepipedon
-dimensional parallelepipedon 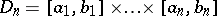 . One introduces the following notation:
. One introduces the following notation:
Let 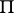 be an arbitrary subdivision of the parallelepipedon by hyperplanes
be an arbitrary subdivision of the parallelepipedon by hyperplanes
into  -dimensional parallelepipeda. Let
-dimensional parallelepipeda. Let 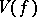 be the least upper bound of sums of the type
be the least upper bound of sums of the type
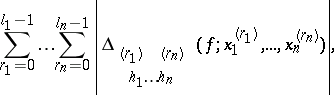 | (*) |
taken over all possible subdivisions of 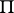 . If
. If 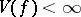 , one says that the function
, one says that the function 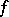 has bounded (finite) Vitali variation on
has bounded (finite) Vitali variation on 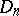 , while the class of all such functions is denoted by
, while the class of all such functions is denoted by 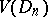 or simply by
or simply by 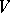 . The class was defined by G. Vitali [1]. The same definition of variation was subsequently proposed by H. Lebesgue [2] and M. Fréchet [3]. A real-valued function
. The class was defined by G. Vitali [1]. The same definition of variation was subsequently proposed by H. Lebesgue [2] and M. Fréchet [3]. A real-valued function 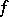 , defined on
, defined on 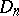 , belongs to the class
, belongs to the class 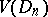 if and only if it can be represented in the form
if and only if it can be represented in the form 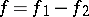 , where the functions
, where the functions 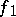 and
and 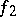 are such that, for each of them, the sums of the type (*), taken without the modulus sign, are non-negative [4] (the analogue of the Jordan decomposition of a function of bounded variation of one variable). The functions of class
are such that, for each of them, the sums of the type (*), taken without the modulus sign, are non-negative [4] (the analogue of the Jordan decomposition of a function of bounded variation of one variable). The functions of class 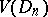 may be used to introduce the multi-dimensional Stieltjes integral. In particular, for any function
may be used to introduce the multi-dimensional Stieltjes integral. In particular, for any function 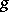 which is continuous on
which is continuous on 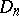 and any function
and any function  of class
of class 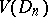 the integral
the integral 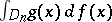 exists [3].
exists [3].
References
| [1] | G. Vitali, "Sui gruppi di punti e sulle funzioni di variabili reali" Atti Accad. Sci. Torino , 43 (1908) pp. 75–92 |
| [2] | H. Lebesgue, "Sur l'intégration des fonctions discontinues" Ann. Sci. École Norm. Sup. (3) , 27 (1910) pp. 361–450 |
| [3] | M. Fréchet, "Extension au cas d'intégrales multiples d'une définition de l'intégrale due à Stieltjes" Nouv. Ann. Math. ser. 4 , 10 (1910) pp. 241–256 |
| [4] | H. Hahn, "Theorie der reellen Funktionen" , 1 , Springer (1921) |
| [5] | F. Riesz, B. Szökefalvi-Nagy, "Functional analysis" , F. Ungar (1955) (Translated from French) |
How to Cite This Entry:
Vitali variation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Vitali_variation&oldid=27961
This article was adapted from an original article by B.I. Golubov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article
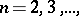 be defined on an
be defined on an  -dimensional parallelepipedon
-dimensional parallelepipedon 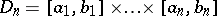 . One introduces the following notation:
. One introduces the following notation:
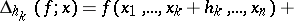
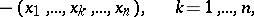
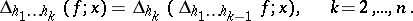
 be an arbitrary subdivision of the parallelepipedon by hyperplanes
be an arbitrary subdivision of the parallelepipedon by hyperplanes
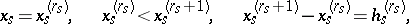
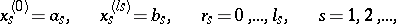
 -dimensional parallelepipeda. Let
-dimensional parallelepipeda. Let 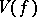 be the least upper bound of sums of the type
be the least upper bound of sums of the type
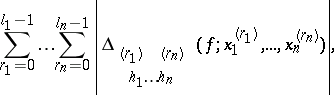
 . If
. If 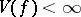 , one says that the function
, one says that the function 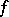 has bounded (finite) Vitali variation on
has bounded (finite) Vitali variation on 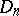 , while the class of all such functions is denoted by
, while the class of all such functions is denoted by 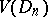 or simply by
or simply by 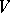 . The class was defined by G. Vitali [1]. The same definition of variation was subsequently proposed by H. Lebesgue [2] and M. Fréchet [3]. A real-valued function
. The class was defined by G. Vitali [1]. The same definition of variation was subsequently proposed by H. Lebesgue [2] and M. Fréchet [3]. A real-valued function 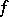 , defined on
, defined on 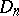 , belongs to the class
, belongs to the class 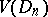 if and only if it can be represented in the form
if and only if it can be represented in the form 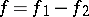 , where the functions
, where the functions 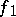 and
and 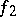 are such that, for each of them, the sums of the type (*), taken without the modulus sign, are non-negative [4] (the analogue of the Jordan decomposition of a function of bounded variation of one variable). The functions of class
are such that, for each of them, the sums of the type (*), taken without the modulus sign, are non-negative [4] (the analogue of the Jordan decomposition of a function of bounded variation of one variable). The functions of class 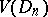 may be used to introduce the multi-dimensional Stieltjes integral. In particular, for any function
may be used to introduce the multi-dimensional Stieltjes integral. In particular, for any function 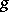 which is continuous on
which is continuous on 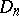 and any function
and any function  of class
of class 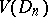 the integral
the integral 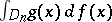 exists [3].
exists [3].