Singular function

A non-constant continuous function of bounded variation whose derivative is zero almost-everywhere on the interval on which it is defined. Singular functions arise as summands in the Lebesgue decomposition of functions of bounded variation. For example, every continuous function 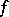of bounded variation on an interval 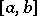can be uniquely written in the form of a sum 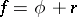, where 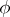is an absolutely-continuous function (cf. Absolute continuity) with 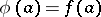and is a singular function or identically zero.

Example. Let 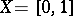. Any 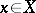can be written in the form

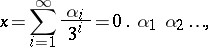where 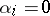, or 2 for . Thus, if , where is the Cantor set, then 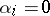or 2 for all 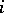. Let 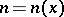be the first subscript for which 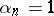; if there are no such subscripts, then one takes 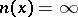. The function

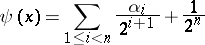is then a monotone singular function on .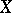

References

[1]	H. Lebesgue, "Leçons sur l'intégration et la récherche des fonctions primitives" , Gauthier-Villars (1928)
[2]	I.P. Natanson, "Theory of functions of a real variable" , 1–2 , F. Ungar (1955–1961) (Translated from Russian)
[3]	P.R. Halmos, "Measure theory" , v. Nostrand (1950)

Comments

The function 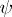is well-defined (i.e. the value 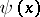does not depend on the chosen representation of ); it is known as Lebesgue's singular function.

References

[a1]	E. Hewitt, K.R. Stromberg, "Real and abstract analysis" , Springer (1965)
[a2]	K.R. Stromberg, "Introduction to classical real analysis" , Wadsworth (1981)