Lebesgue decomposition

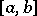The Lebesgue decomposition of a function of bounded variation is a canonical representation of this function as a sum of at most three terms. If is a function of bounded variation on the interval , then it can be represented in the form

where 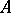is an absolutely-continuous function (see Absolute continuity), 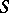is a singular function and 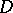is a jump function. In certain cases, for example, if 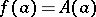, this representation is unique. The Lebesgue decomposition was established by H. Lebesgue (1904) (see [1]).

References

[1]	H. Lebesgue, "Leçons sur l'intégration et la récherche des fonctions primitives" , Gauthier-Villars (1928)
[2]	I.P. Natanson, "Theorie der Funktionen einer reellen Veränderlichen" , H. Deutsch , Frankfurt a.M. (1961) (Translated from Russian)
[3]	P.R. Halmos, "Measure theory" , v. Nostrand (1950)

B.I. Golubov

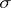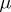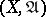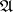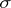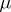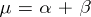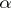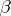The Lebesgue decomposition of a -finite signed measure defined on a measurable space ( is a -algebra), with respect to a -finite signed measure defined on this space, is a representation of in the form , where and are 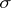-finite signed measures, 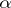is absolutely continuous (cf. Absolute continuity) with respect to , and is singular with respect to (cf. Mutually-singular measures). Such a representation is always possible and unique.

References

[1]	P.R. Halmos, "Measure theory" , v. Nostrand (1950)
[2]	N. Dunford, J.T. Schwartz, "Linear operators" , 1–3 , Interscience (1958–1971)