Jordan decomposition (of an endomorphism)
The Jordan decomposition of a function 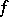 of bounded variation is the representation of
of bounded variation is the representation of 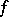 in the form
in the form
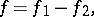 |
where 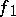 and
and 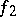 are monotone increasing functions. A Jordan decomposition is also the representation of a signed measure or a charge
are monotone increasing functions. A Jordan decomposition is also the representation of a signed measure or a charge 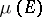 on measurable sets
on measurable sets  as a difference of measures,
as a difference of measures,
 |
where at least one of the measures (cf. Measure) 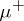 and
and 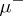 is finite. Established by C. Jordan.
is finite. Established by C. Jordan.
References
| [1] | C. Jordan, "Cours d'analyse" , 1 , Gauthier-Villars (1893) MR1188188 MR1188187 MR1188186 MR0710200 |
| [2] | P.R. Halmos, "Measure theory" , v. Nostrand (1950) MR0033869 Zbl 0040.16802 |
| [3] | I.P. Natanson, "Theorie der Funktionen einer reellen Veränderlichen" , H. Deutsch , Frankfurt a.M. (1961) (Translated from Russian) MR0640867 MR0409747 MR0259033 MR0063424 Zbl 0097.26601 |
M.I. Voitsekhovskii
the Jordan decomposition of an endomorphism 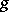 of a finite-dimensional vector space is the representation of
of a finite-dimensional vector space is the representation of 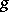 as the sum of a semi-simple and a nilpotent endomorphism that commute with each other:
as the sum of a semi-simple and a nilpotent endomorphism that commute with each other:  . The endomorphisms
. The endomorphisms 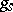 and
and 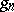 are said to be the semi-simple and the nilpotent component of the Jordan decomposition of
are said to be the semi-simple and the nilpotent component of the Jordan decomposition of 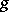 . This decomposition is called the additive Jordan decomposition. (A semi-simple endomorphism is one having a basis of eigen vectors for some extension of the ground field, a nilpotent endomorphism is one some power of which is the zero endomorphism.) If in some basis of the space the matrix
. This decomposition is called the additive Jordan decomposition. (A semi-simple endomorphism is one having a basis of eigen vectors for some extension of the ground field, a nilpotent endomorphism is one some power of which is the zero endomorphism.) If in some basis of the space the matrix 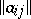 of
of 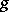 is a Jordan matrix (i.e., a matrix in Jordan canonical form), and
is a Jordan matrix (i.e., a matrix in Jordan canonical form), and 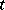 is an endomorphism such that the matrix
is an endomorphism such that the matrix 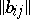 of
of 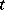 in the same basis has
in the same basis has 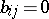 for
for 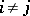 and
and 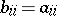 for all
for all 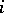 , then
, then
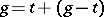 |
is the Jordan decomposition of 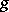 with
with 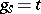 and
and 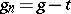 .
.
The Jordan decomposition exists and is unique for any endomorphism 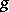 of a vector space
of a vector space 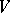 over an algebraically closed field
over an algebraically closed field 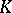 . Moreover,
. Moreover, 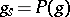 and
and 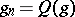 for some polynomials
for some polynomials 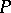 and
and 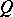 over
over  (depending on
(depending on 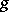 ) with constant terms equal to zero. If
) with constant terms equal to zero. If 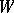 is a
is a 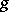 -invariant subspace of
-invariant subspace of 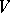 , then
, then 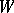 is invariant under
is invariant under 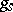 and
and  , and
, and
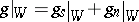 |
is the Jordan decomposition of 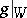 (here
(here  means restriction to
means restriction to 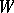 ). If
). If 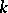 is a subfield of
is a subfield of 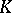 and
and 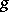 is rational over
is rational over 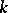 (with respect to some
(with respect to some 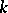 -structure on
-structure on 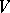 ), then
), then 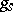 and
and 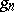 need not be rational over
need not be rational over 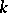 ; one may only assert that
; one may only assert that 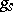 and
and 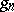 are rational over
are rational over 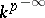 , where
, where 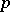 is the characteristic exponent of
is the characteristic exponent of 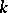 (for
(for 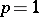 ,
, 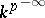 is
is  , and for
, and for 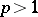 it is the set of all elements of
it is the set of all elements of 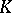 that are purely inseparable over
that are purely inseparable over 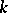 , cf. Separable extension).
, cf. Separable extension).
If 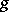 is an automorphism of
is an automorphism of 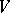 , then
, then 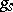 is also an automorphism of
is also an automorphism of 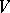 , and
, and
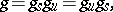 |
where 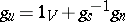 and
and 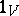 is the identity automorphism of
is the identity automorphism of  . The automorphism
. The automorphism 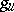 is unipotent, that is, all its eigen values are equal to one. Every representation of
is unipotent, that is, all its eigen values are equal to one. Every representation of 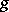 as a product of commuting semi-simple and unipotent automorphisms coincides with the representation
as a product of commuting semi-simple and unipotent automorphisms coincides with the representation 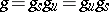 already described. This representation is called the multiplicative Jordan decomposition of the automorphism
already described. This representation is called the multiplicative Jordan decomposition of the automorphism 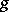 , and
, and 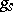 and
and 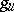 are called the semi-simple and unipotent components of
are called the semi-simple and unipotent components of 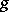 . If
. If 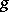 is rational over
is rational over 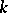 , then
, then 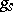 and
and 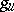 are rational over
are rational over  . If
. If 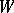 is a
is a 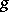 -invariant subspace of
-invariant subspace of 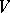 , then
, then 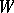 is invariant under
is invariant under 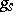 and
and 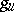 , and
, and
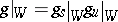 |
is the multiplicative Jordan decomposition of 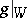 .
.
The concept of a Jordan decomposition can be generalized to locally finite endomorphisms of an infinite-dimensional vector space 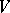 , that is, endomorphisms
, that is, endomorphisms 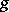 such that
such that  is generated by finite-dimensional
is generated by finite-dimensional 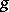 -invariant subspaces. For such
-invariant subspaces. For such 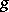 , there is one and only one decomposition of
, there is one and only one decomposition of 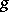 as a sum
as a sum 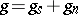 (and in the case of an automorphism, one and only one decomposition of
(and in the case of an automorphism, one and only one decomposition of 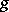 as a product
as a product 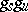 ) of commuting locally finite semi-simple and nilpotent endomorphisms (semi-simple and unipotent automorphisms, respectively), that is, endomorphisms (automorphisms) such that every finite-dimensional
) of commuting locally finite semi-simple and nilpotent endomorphisms (semi-simple and unipotent automorphisms, respectively), that is, endomorphisms (automorphisms) such that every finite-dimensional 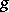 -invariant subspace
-invariant subspace 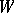 of
of 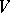 is invariant under
is invariant under 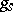 and
and 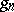 (
(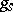 and
and 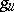 , respectively) and
, respectively) and 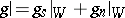 (
(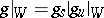 , respectively) is the Jordan decomposition of
, respectively) is the Jordan decomposition of 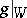 .
.
This extension of the concept of a Jordan decomposition allows one to introduce the concept of a Jordan decomposition in algebraic groups and algebras. Let 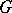 be an affine algebraic group over
be an affine algebraic group over 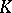 (cf. Affine group), let
(cf. Affine group), let 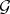 be its Lie algebra, let
be its Lie algebra, let 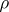 be the representation of
be the representation of 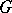 in the group of automorphisms of the algebra
in the group of automorphisms of the algebra 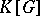 of regular functions on
of regular functions on 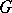 defined by right translations, and let
defined by right translations, and let 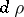 be its derivation. For arbitrary
be its derivation. For arbitrary 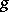 in
in 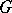 and
and 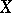 in
in 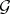 , the endomorphisms
, the endomorphisms 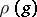 and
and 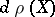 of the vector space
of the vector space 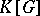 are locally finite, so that one can speak of their Jordan decompositions:
are locally finite, so that one can speak of their Jordan decompositions:
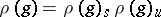 |
and
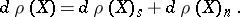 |
One of the important results in the theory of algebraic groups is that the Jordan decomposition just indicated is realized by the use of elements of 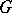 and
and 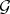 , respectively. More exactly, there exist unique elements
, respectively. More exactly, there exist unique elements 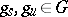 and
and 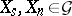 such that
such that
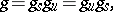 | (1) |
 | (2) |
and
 |
 |
The decomposition (1) is called the Jordan decomposition in the algebraic group 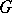 , and (2) the Jordan decomposition in the algebraic Lie algebra
, and (2) the Jordan decomposition in the algebraic Lie algebra 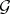 . If
. If 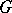 is defined over a subfield
is defined over a subfield  of
of 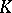 and the element
and the element 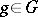 (
(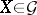 , respectively) is rational over
, respectively) is rational over 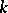 , then
, then 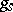 and
and 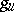 (
(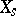 and
and 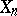 , respectively) are rational over
, respectively) are rational over 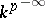 . Moreover, if
. Moreover, if 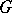 is realized as a closed subgroup of the general linear group
is realized as a closed subgroup of the general linear group 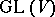 of automorphisms of some finite-dimensional vector space
of automorphisms of some finite-dimensional vector space 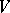 (and thus
(and thus 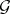 is realized as a subalgebra of the Lie algebra of
is realized as a subalgebra of the Lie algebra of 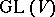 ), then the Jordan decomposition (1) of
), then the Jordan decomposition (1) of 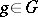 coincides with the multiplicative decomposition introduced above for
coincides with the multiplicative decomposition introduced above for 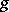 , while the decomposition (2) for
, while the decomposition (2) for 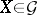 coincides with the additive Jordan decomposition for
coincides with the additive Jordan decomposition for 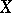 (considered as endomorphisms of
(considered as endomorphisms of 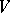 ). If
). If 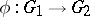 is a rational homomorphism of affine algebraic groups and
is a rational homomorphism of affine algebraic groups and 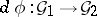 is the corresponding homomorphism of their Lie algebras, then
is the corresponding homomorphism of their Lie algebras, then
 |
 |
for arbitrary 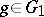 ,
,  .
.
The concept of a Jordan decomposition in algebraic groups and algebraic Lie algebras allows one to introduce the definitions of a semi-simple and a unipotent (nilpotent, respectively) element in an arbitrary affine algebraic group (algebraic Lie algebra, respectively). An element 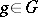 is said to be semi-simple if
is said to be semi-simple if  , and unipotent if
, and unipotent if 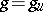 ; an element
; an element 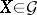 is said to be semi-simple if
is said to be semi-simple if 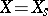 and nilpotent if
and nilpotent if  . If
. If 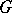 is defined over
is defined over 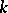 , then
, then
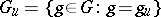 |
is a 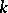 -closed subset of
-closed subset of  , and
, and
 |
is a 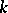 -closed subset of
-closed subset of 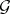 . In general,
. In general,
 |
is not a closed set, but if 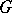 is commutative, then
is commutative, then 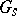 and
and 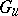 are closed subgroups and
are closed subgroups and 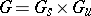 . The sets
. The sets 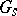 and
and 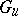 in an arbitrary affine algebraic group are invariant under inner automorphisms, and the study of decompositions of these sets into classes of conjugate elements is a subject of special investigations [3].
in an arbitrary affine algebraic group are invariant under inner automorphisms, and the study of decompositions of these sets into classes of conjugate elements is a subject of special investigations [3].
References
| [1] | A. Borel, "Linear algebraic groups" , Benjamin (1969) MR0251042 Zbl 0206.49801 Zbl 0186.33201 |
| [2] | E.R. Kolchin, "Algebraic matrix groups and the Picard–Vessiot theory of homogeneous linear ordinary differential equations" Ann. of Math. , 49 (1948) pp. 1–42 |
| [3] | A. Borel (ed.) R. Carter (ed.) C.W. Curtis (ed.) N. Iwahori (ed.) T.A. Springer (ed.) R. Steinberg (ed.) , Seminar on algebraic groups and related finite groups , Lect. notes in math. , 131 , Springer (1970) Zbl 0192.36201 |
V.L. Popov
Comments
References
| [a1] | R. Steinberg, "Conjugacy classes in algebraic groups" , Lect. notes in math. , 366 , Springer (1974) MR0352279 Zbl 0281.20037 |
Jordan decomposition (of an endomorphism). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Jordan_decomposition_(of_an_endomorphism)&oldid=27713