Singular measures
From Encyclopedia of Mathematics
Revision as of 13:32, 12 August 2012 by Camillo.delellis (talk | contribs) (moved Mutually-singular measures to Singular measures: More common name. I will redirect the old page.)
Two (positive) measures 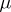 and
and  , defined on a locally compact space
, defined on a locally compact space 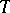 , such that
, such that 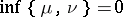 .
.
Two measures 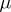 and
and  are mutually singular if and only if there exist in
are mutually singular if and only if there exist in 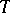 two disjoint sets
two disjoint sets 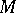 and
and 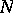 such that
such that 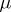 is concentrated on
is concentrated on 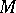 and
and  on
on 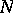 .
.
References
| [1] | N. Bourbaki, "Elements of mathematics. Integration" , Addison-Wesley (1975) pp. Chapt.6;7;8 (Translated from French) |
Comments
The second characterization in the main article above holds if  and
and  are
are  -additive
-additive 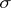 -finite measures on an abstract measurable space, and
-finite measures on an abstract measurable space, and 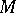 and
and 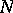 belong to the
belong to the 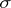 -field.
-field.
Mutually-singular measures are also called singular measures or orthogonal measures.
Instead of "concentrated on" one also uses "supported in" (cf. also Support of a measure).
References
| [a1] | P.R. Halmos, "Measure theory" , v. Nostrand (1950) |
| [a2] | E. Hewitt, K.R. Stromberg, "Real and abstract analysis" , Springer (1965) |
How to Cite This Entry:
Singular measures. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Singular_measures&oldid=27499
Singular measures. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Singular_measures&oldid=27499
This article was adapted from an original article by M.I. Voitsekhovskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article