Lebesgue set
From Encyclopedia of Mathematics
of a locally summable function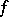 
defined on an open set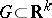 
The set of points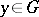 
at which
 |
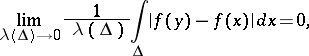where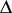 
is a closed cube containing the point 
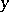and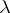 
is the Lebesgue measure. Here the function 
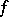can be real- or vector-valued.
Comments
When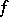 
is real-valued and locally integrable, the complement of its Lebesgue set has (Lebesgue) measure zero. This is used in the study of differentiability via maximal functions, cf. [a1].
References
| [a1] | E.M. Stein, "Singular integrals and differentiability properties of functions" , Princeton Univ. Press (1970) |
| [a2] | W. Rudin, "Real and complex analysis" , McGraw-Hill (1978) pp. 24 |
How to Cite This Entry:
Lebesgue set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lebesgue_set&oldid=27420
Lebesgue set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lebesgue_set&oldid=27420
This article was adapted from an original article by V.V. Sazonov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article