Approximate derivative

A generalization of the concept of a derivative, where the ordinary limit is replaced by an approximate limit. If, for a function 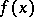of a real variable , the limit

exists, then it is called the approximate derivative of the function 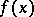at and is denoted by . In the simplest case is a real-valued function; in general it is a vector-valued function. An approximate derivative may be finite or infinite. The classical rules for the differentiation of a sum, a difference, a product, and a quotient of functions apply to finite approximate derivatives; the theorem on the differentiation of a composite function does not apply in general. The concept of an approximate derivative was introduced by >A.Ya. Khinchin in 1916.

Approximate Dini derivatives are defined by analogy with ordinary Dini derivatives (cf. Dini derivative): 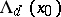— lim sup from the right; 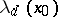— lim inf from the right; 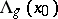— lim sup from the left; 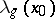— lim inf from the left; for example,

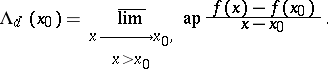The following Denjoy–Khinchin theorems apply. If a real-valued function 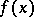is finite and Lebesgue-measurable on a set 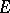, then, at almost any point of this set, either 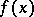has a finite approximate derivative, or

If

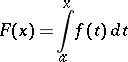is a Denjoy–Khinchin integral, then 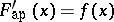almost-everywhere in the interval under consideration (an ordinary derivative need not exist on a set of positive measure). This theorem explains the role played by approximate derivatives in the theory of integrals.

There exist continuous functions without an ordinary or an approximate derivative at any point of a given interval.

Approximate partial derivatives of functions of several real variables are considered as well.

References

[1]	S. Saks, "Theory of the integral" , Hafner (1952) (Translated from French)

Comments

For other references see Approximate limit.