Approximate continuity
A generalization of the concept of continuity in which the ordinary limit is replaced by an approximate limit. A function 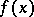 is called approximately continuous at a point
is called approximately continuous at a point 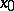 if
if
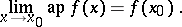 |
In the simplest case, 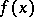 is a real-valued function of the points of an
is a real-valued function of the points of an  -dimensional Euclidean space (in general it is a vector-valued function). The following theorems apply. 1) A real-valued function
-dimensional Euclidean space (in general it is a vector-valued function). The following theorems apply. 1) A real-valued function 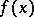 is Lebesgue-measurable on a set
is Lebesgue-measurable on a set 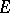 if and only if it is approximately continuous almost-everywhere on
if and only if it is approximately continuous almost-everywhere on 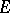 (the Stepanov–Denjoy theorem). 2) For any bounded Lebesgue-measurable function
(the Stepanov–Denjoy theorem). 2) For any bounded Lebesgue-measurable function  one has, at each point
one has, at each point 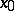 ,
,
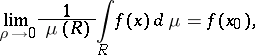 |
where 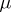 is the
is the  -dimensional Lebesgue measure,
-dimensional Lebesgue measure, 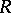 is an
is an  -dimensional non-degenerate segment containing
-dimensional non-degenerate segment containing 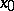 , and
, and 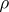 is its diameter.
is its diameter.
References
| [1] | S. Saks, "Theory of the integral" , Hafner (1952) (Translated from French) |
Comments
For other references see Approximate limit.
Approximate continuity. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Approximate_continuity&oldid=27390