Liouville normal form

A way of writting a second-order ordinary linear differential equation

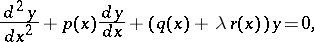(1)

in the form

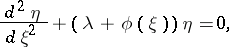(2)

where 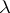is parameter. If 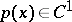, 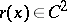and 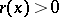, then equation (1) reduces to the Liouville normal form (2) by means of the substitution

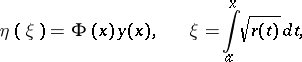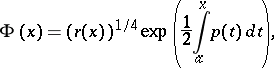which is called the Liouville transformation (introduced in [1]). The Liouville normal form plays an important role in the investigation of the asymptotic behaviour of solutions of (1) for large values of the parameter or the argument, and in the investigation of the asymptotics of eigen functions and eigen values of the Sturm–Liouville problem (see [3]).

References

[1]	J. Liouville, J. Math. Pures Appl. , 2 (1837) pp. 16–35
[2]	E. Kamke, "Differentialgleichungen: Lösungen und Lösungsmethoden" , 1. Gewöhnliche Differentialgleichungen , Chelsea, reprint (1947)
[3]	E.C. Titchmarsh, "Eigenfunction expansions associated with second-order differential equations" , 1–2 , Clarendon Press (1946–1948)

References

[a1]	E.L. Ince, "Ordinary differential equations" , Dover, reprint (1956)