Airy equation

The second-order linear ordinary differential equation

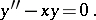It occurred first in G.B. Airy's research in optics [1]. Its general solution can be expressed in terms of Bessel functions of order :

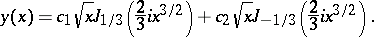Since the Airy equation plays an important role in various problems of physics, mechanics and asymptotic analysis, its solutions are regarded as forming a distinct class of special functions (see Airy functions).

The solutions of the Airy equation in the complex plane ,

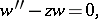have the following fundamental properties:

1) Every solution is an entire function of and can be expanded in a power series

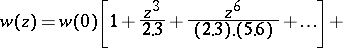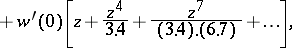which converges for all .

2) If 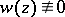is a solution of the Airy equation, then so are 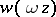and 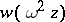, where 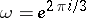, and any two of these solutions are linearly independent. The following identity holds:

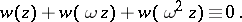References

[1]	G.B. Airy, "On the intensity of light in the neighbourhood of a caustic" Trans. Cambridge Philos. Soc. , 6 (1838) pp. 379–402
[2]	V.M. Babich, V.S. Buldyrev, "Asymptotic methods in the diffraction of short waves" , Moscow (1972) (In Russian) (Translation forthcoming: Springer)
[3]	M. Abramowitz (ed.) I.A. Stegun (ed.) , Handbook of mathematical functions , Appl. Math. Series , 55 , Nat. Bureau of Standards,, U.S. Department Commerce (1964)