Wilson theorem

Let 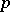be a prime number. Then the number 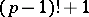is divisible by 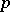. The theorem was first formulated by E. Waring (1770) and is, according to him, due to J. Wilson. It was proved by J.L. Lagrange in 1771. A primality test for integers follows from Wilson's theorem: A natural number will be prime if and only if

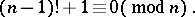This test is not recommended for practical use, since the factorial involved rapidly becomes very large.

References

[1]	A.A. Bukhshtab, "Number theory" , Moscow (1966) (In Russian)
[2]	E. Trost, "Primzahlen" , Birkhäuser (1953)
[3]	I.M. [I.M. Vinogradov] Winogradow, "Elemente der Zahlentheorie" , R. Oldenbourg (1956) (Translated from Russian)

Comments

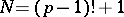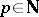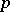In fact, also the converse is true (and usually also called Wilson's theorem): Let , with . Then is divisible by if and only if 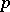is a prime number.

References

[a1]	D. Shanks, "Solved and unsolved problems in number theory" , Chelsea, reprint (1978)
[a2]	M.R. Schroeder, "Number theory in science and communication" , Springer (1984) pp. 103
[a3]	G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Clarendon Press (1960) pp. 68