Abel differential equation
The ordinary differential equation
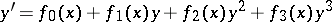 |
(Abel's differential equation of the first kind) or
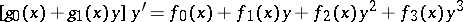 |
(Abel's differential equation of the second kind). These equations arose in the context of the studies of N.H. Abel [1] on the theory of elliptic functions. Abel's differential equations of the first kind represent a natural generalization of the Riccati equation.
If 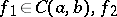 and
and 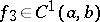 and
and 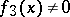 for
for 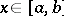 , then Abel's differential equation of the first kind can be reduced to the normal form
, then Abel's differential equation of the first kind can be reduced to the normal form 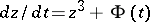 by substitution of variables [2]. In the general case, Abel's differential equation of the first kind cannot be integrated in closed form, though this is possible in special cases [2]. If
by substitution of variables [2]. In the general case, Abel's differential equation of the first kind cannot be integrated in closed form, though this is possible in special cases [2]. If 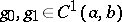 and
and 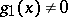 ,
, 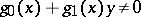 , Abel's differential equation of the second kind can be reduced to Abel's differential equation of the first kind by substituting
, Abel's differential equation of the second kind can be reduced to Abel's differential equation of the first kind by substituting 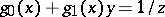 .
.
Abel's differential equations of the first and second kinds, as well as their further generalizations
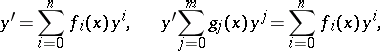 |
have been studied in detail in the complex domain (see, for example, [3]).
References
| [1] | N.H. Abel, "Précis d'une théorie des fonctions elliptiques" J. Reine Angew. Math. , 4 (1829) pp. 309–348 |
| [2] | E. Kamke, "Differentialgleichungen: Lösungen und Lösungsmethoden" , 1. Gewöhnliche Differentialgleichungen , Chelsea, reprint (1971) |
| [3] | V.V. Golubev, "Vorlesungen über Differentialgleichungen im Komplexen" , Deutsch. Verlag Wissenschaft. (1958) (Translated from Russian) |
Abel differential equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Abel_differential_equation&oldid=27047