Equivalence relation
From Encyclopedia of Mathematics
A binary relation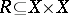 
on a set 
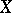with the following properties:
1) for all 
: 
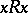(reflexivity);
2) 
(symmetry);
3) 
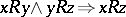(transitivity).
If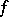 
maps the set 
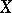into a set 
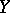, then the relation 
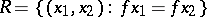is an equivalence.
For any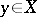 
the set 
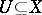consisting of all 
equivalent to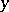 
is called the equivalence class of 
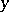. Any two equivalence classes either are disjoint or coincide, that is, any equivalence defines a partition (decomposition) of 
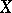, and vice versa.
How to Cite This Entry:
Equivalence relation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Equivalence_relation&oldid=26964
Equivalence relation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Equivalence_relation&oldid=26964
This article was adapted from an original article by V.N. Grishin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article