Cartan matrix
The Cartan matrix of a finite-dimensional semi-simple Lie algebra 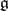 over an algebraically closed field
over an algebraically closed field 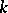 of characteristic
of characteristic  is a matrix
is a matrix
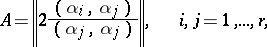 |
where  is some system of simple roots of
is some system of simple roots of 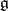 with respect to a fixed Cartan subalgebra
with respect to a fixed Cartan subalgebra 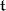 and
and 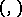 is the scalar product on the dual space of
is the scalar product on the dual space of 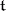 defined by the Killing form on
defined by the Killing form on 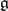 . (For the Cartan matrix of an arbitrary system of roots see Root system.) Up to a transformation induced by a permutation of the indices
. (For the Cartan matrix of an arbitrary system of roots see Root system.) Up to a transformation induced by a permutation of the indices 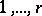 , a Cartan matrix is an invariant of
, a Cartan matrix is an invariant of 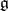 , that is, it does not depend on the choice of
, that is, it does not depend on the choice of 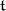 or the system of simple roots. This invariant completely determines
or the system of simple roots. This invariant completely determines  : Two semi-simple Lie algebras are isomorphic if and only if their Cartan matrices are the same, up to a transformation induced by permutation of the indices. A semi-simple Lie algebra is simple if and only if its Cartan matrix is indecomposable, that is, not expressible as a block-diagonal matrix after some permutation of indices.
: Two semi-simple Lie algebras are isomorphic if and only if their Cartan matrices are the same, up to a transformation induced by permutation of the indices. A semi-simple Lie algebra is simple if and only if its Cartan matrix is indecomposable, that is, not expressible as a block-diagonal matrix after some permutation of indices.
Let 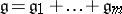 be a decomposition of
be a decomposition of 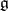 into a direct sum of simple subalgebras and let
into a direct sum of simple subalgebras and let 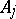 be the Cartan matrix of the simple Lie algebra
be the Cartan matrix of the simple Lie algebra  . Then the block-diagonal matrix
. Then the block-diagonal matrix
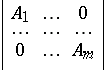 |
is the Cartan matrix of 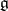 . (For the explicit form of the Cartan matrix of simple Lie algebras, see Lie algebra, semi-simple.)
. (For the explicit form of the Cartan matrix of simple Lie algebras, see Lie algebra, semi-simple.)
The entries  of a Cartan matrix have the following properties:
of a Cartan matrix have the following properties:
 | (1) |
The Cartan matrix is closely related to the description of  in terms of generators and relations. Namely, there exist in
in terms of generators and relations. Namely, there exist in 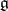 linearly independent generators
linearly independent generators 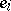 ,
, 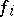 ,
, 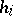 ,
, 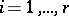 (the so-called canonical generators), connected by the following relations:
(the so-called canonical generators), connected by the following relations:
 | (2) |
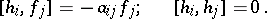 |
Any two systems of canonical generators can be transformed one into the other by automorphism of 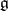 . In addition to (2), the canonical generators satisfy the relations
. In addition to (2), the canonical generators satisfy the relations
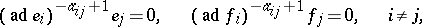 | (3) |
where, by definition, 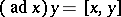 . For the chosen system of generators
. For the chosen system of generators 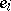 ,
, 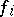 ,
,  ,
, 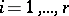 , relations (2) and (3) are defining for
, relations (2) and (3) are defining for  (see [2]).
(see [2]).
For any matrix  satisfying (1), the Lie algebra
satisfying (1), the Lie algebra 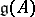 over the field
over the field  with generators
with generators 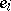 ,
, 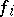 ,
, 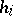 ,
,  , and defining relations (2) and (3) is finite-dimensional if and only if
, and defining relations (2) and (3) is finite-dimensional if and only if  is the Cartan matrix of a semi-simple Lie algebra [3].
is the Cartan matrix of a semi-simple Lie algebra [3].
References
| [1] | N. Jacobson, "Lie algebras" , Interscience (1962) ((also: Dover, reprint, 1979)) |
| [2] | J.-P. Serre, "Algèbres de Lie semi-simples complexes" , Benjamin (1966) |
| [3] | V.G. [V.G. Kats] Kac, "Simple irreducible graded Lie algebras of finite growth" Math. USSR Izv. , 2 : 6 (1968) pp. 1271–1311 Ivz. Akad. Nauk SSSR Ser. Mat. , 32 : 6 (1968) pp. 1323–1367 |
Comments
A matrix 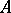 satisfying (1) defines a finite-dimensional Lie algebra if and only if it is positive definite; in other cases, notably the semi-positive definite case, other interesting algebras arise, cf. Kac–Moody algebra, [a2].
satisfying (1) defines a finite-dimensional Lie algebra if and only if it is positive definite; in other cases, notably the semi-positive definite case, other interesting algebras arise, cf. Kac–Moody algebra, [a2].
Let 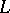 be a semi-simple Lie algebra over an algebraically closed field of characteristic zero. Then a set of generators
be a semi-simple Lie algebra over an algebraically closed field of characteristic zero. Then a set of generators 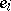 ,
, 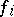 ,
, 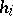 such that (2) holds is also called a set of Chevalley generators or a Chevalley basis. That such a set of generators exists is Chevalley's theorem. The result that the relations (2) and (3) together define the Lie algebra is often called Serre's theorem.
such that (2) holds is also called a set of Chevalley generators or a Chevalley basis. That such a set of generators exists is Chevalley's theorem. The result that the relations (2) and (3) together define the Lie algebra is often called Serre's theorem.
References
| [a1] | J.E. Humphreys, "Introduction to Lie algebras and representation theory" , Springer (1972) |
| [a2] | V.G. Kac, "Infinite dimensional Lie algebras" , Cambridge Univ. Press (1985) |
The Cartan matrix of a finite-dimensional associative algebra  with a unit over a field
with a unit over a field 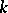 is the matrix
is the matrix 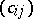 ,
, 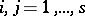 , defined by a complete set
, defined by a complete set  of finite-dimensional irreducible left
of finite-dimensional irreducible left 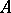 -modules. Specifically,
-modules. Specifically,  is the multiplicity of occurrence of
is the multiplicity of occurrence of 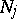 in a composition series of an indecomposable projective left
in a composition series of an indecomposable projective left 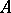 -module
-module 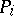 for which
for which 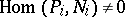 . Such a module
. Such a module 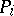 exists for each
exists for each 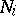 and is uniquely defined up to an isomorphism.
and is uniquely defined up to an isomorphism.
In certain cases the Cartan matrix 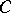 turns out to be symmetric, positive definite, and even
turns out to be symmetric, positive definite, and even 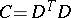 , where
, where 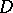 is an integral, not necessarily square, matrix (and
is an integral, not necessarily square, matrix (and  denotes taking the transpose matrix). Such is the case for the Cartan matrix of the group algebra
denotes taking the transpose matrix). Such is the case for the Cartan matrix of the group algebra 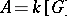 of a finite group
of a finite group 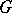 over a field
over a field  of characteristic
of characteristic 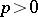 (see [1]); in this case the
(see [1]); in this case the 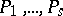 form a complete set of non-isomorphic principal indecomposable left
form a complete set of non-isomorphic principal indecomposable left  -modules, that is, indecomposable
-modules, that is, indecomposable 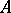 -modules into which the left
-modules into which the left 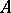 -modules
-modules 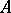 is decomposed as a direct sum. Another example when such an equality holds for a Cartan matrix:
is decomposed as a direct sum. Another example when such an equality holds for a Cartan matrix: 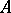 is the restricted universal enveloping algebra of a Lie algebra
is the restricted universal enveloping algebra of a Lie algebra 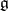 over an algebraically closed field of characteristic
over an algebraically closed field of characteristic 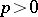 , obtained from a semi-simple complex Lie algebra
, obtained from a semi-simple complex Lie algebra 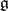 by reduction to characteristic
by reduction to characteristic 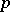 (see [2]).
(see [2]).
References
| [1] | C.W. Curtis, I. Reiner, "Representation theory of finite groups and associative algebras" , Interscience (1962) |
| [2] | J.E. Humphreys, "Modular representations of classical Lie algebras and semi-simple groups" J. of Algebra , 19 (1971) pp. 51–79 |
Cartan matrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cartan_matrix&oldid=26773