Totally-bounded space

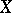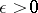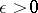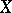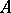A metric space that, for any , can be represented as the union of a finite number of sets with diameters smaller than . An equivalent condition is the following: For each there exists in a finite -net, i.e. a finite set such that the distance of each point of 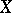from some point of 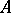is less than . Totally-bounded spaces are those, and only those, metric spaces that can be represented as subspaces of compact metric spaces (cf. Compact space). The metric totally-bounded spaces, considered as topological spaces, exhaust all regular spaces (cf. Regular space) with a countable base. A subspace of a Euclidean space is totally bounded if and only if it is bounded. The converse is not true: An infinite space in which the distance between any two points is one, as well as a sphere and a ball of a Hilbert space, are bounded, but not totally bounded, metric spaces. The significance of the concept of a totally-bounded space may be illustrated by the following theorem: A metric space is a compactum if and only if it is totally bounded and complete. The metric completion of a metric totally-bounded space is compact. The image of a totally-bounded space under a uniformly continuous mapping is a totally-bounded space.

References

[1]	J.L. Kelley, "General topology" , Springer (1975)
[2]	F. Hausdorff, "Grundzüge der Mengenlehre" , Leipzig (1914) (Reprinted (incomplete) English translation: Set theory, Chelsea (1978))
[3]	P.S. Aleksandrov, "Einführung in die Mengenlehre und die Theorie der reellen Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian)
[4]	A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , 1–2 , Graylock (1957–1961) (Translated from Russian)

References

[a1]	R. Engelking, "General topology" , Heldermann (1989)