Weierstrass coordinates

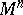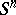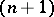A type of coordinates in an elliptic space. Let be an elliptic space obtained by the identification of diametrically-opposite points of the unit sphere in -dimensional Euclidean space. The Weierstrass coordinates 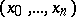of a point in 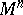are the orthogonal Cartesian coordinates of the point of 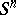that corresponds to it. Since the isometric mapping of 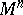into 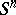is not single-valued, Weierstrass coordinates are defined up to sign. A hyperplane in 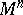is given by a homogeneous linear equation

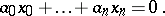Named after K. Weierstrass, who used these coordinates in his courses on Lobachevskii geometry in 1872.

Comments

These coordinates for elliptic space can be normalized so that

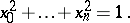The analogous Weierstrass coordinates for hyperbolic space satisfy

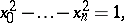with the same equation for a hyperplane.

References

[a1]	H. Liebmann, "Nichteuklidische Geometrie" , Göschen (1912) pp. 114–119
[a2]	H.S.M. Coxeter, "Non-Euclidean geometry" , Univ. Toronto Press (1965) pp. 121, 281