Wald identity

An identity in sequential analysis which states that the mathematical expectation of the sum of a random number of independent, identically-distributed random variables is equal to the product of the mathematical expectations and :

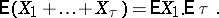A sufficient condition for the Wald identity to be valid is that the mathematical expectations and in fact exist, and for the random variable to be a Markov time (i.e. for any 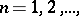the event 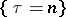is determined by the values of the random variables 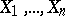or, which is the same thing, the event 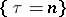belongs to the 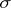-algebra generated by the random variables ). Wald's identity is a particular case of a fundamental theorem in sequential analysis stating that

(*)

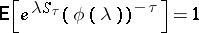for all complex 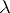for which 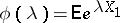exists and . It was established by A. Wald [1].

References

[1]	A. Wald, "Sequential analysis" , Wiley (1952)
[2]	W. Feller, "An introduction to probability theory and its applications" , 1 , Wiley (1957) pp. Chapt.14

Comments

The general result (*) is (also) referred to as Wald's formula.

References

[a1]	A.V. [A.V. Skorokhod] Skorohod, "Random processes with independent increments" , Kluwer (1991) pp. 23 (Translated from Russian)