Degenerate elliptic equation

A partial differential equation

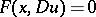(1)

where the real-valued function 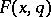satisfies the condition

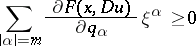(2)

for all real 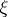, and there exists a 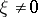for which (2) becomes an equality. Here, is an -dimensional vector 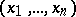; is the unknown function; 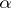is a multi-index 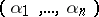; 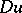is a vector with components

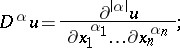the derivatives in equation (1) are of an order not exceeding 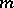; the 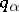are the components of a vector 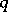; 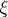is an -dimensional vector 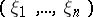; and 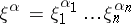. If strict inequality in equation (2) holds for all and 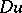and for all real 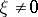, equation (1) is elliptic at 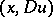. Equation (1) degenerates at the points 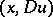at which inequality (2) becomes an equality for any real 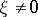. If equality holds only on the boundary of the domain under consideration, the equation is called degenerate on the boundary of the domain. The most thoroughly studied equations are second-order degenerate elliptic equations

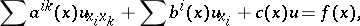where the matrix 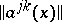is non-negative definite for all -values under consideration.

See also Degenerate partial differential equation and the references given there.